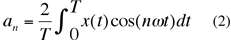1The link, if there were one, between the form and the function of objects that surround us has been one of the most enduring and intriguing of questions in the realm of science. The present study explores a methodology to analyze shapes of watershed outlines, and represents an attempt to contribute to the understanding of the their relationships with the underlying geomorphologic processes.
2A watershed acts as an interface between the rainfall field and the outlet where the river discharge is recorded (DeBarry, 2004). The stream network, the underground soil, and the boundaries defining the drainage area form parts of a watershed (Douvinet et al., 2008). These components, critical as they are in the watershed system, are yet to be adequately understood in their many dimensions. For instance, how can we compare watershed boundaries in terms of shape? How may two watersheds differing in boundary shape, but similar in respect of stream networks and underground substrates, actually differ in hydrological responses?
3During a rainfall event, watershed shape impacts the shape of the resulting hydrograph, although this information cannot always be derived from the river network (Rodriguez-Iturbe and Rinaldo, 1997). For instance, the basin lagtime of a pear-shaped watershed is known to be shorter when the outlet is in the rounded part than in the stem end (Réméniéras, 1960; Gregory and Walling, 1973; fig. 1). While the characteristics of a river network might furnish it, the watershed boundaries capture information from the surface beyond the network sources as they collect the rain water. We would need a method to describe watershed boundaries to quantify accurately such information.
4Methodologically and historically, morphometrics or the quantitative studies of form can be divided into two approaches, comparison of ‘size’ being the aim of one, while comparison of ‘shape’ is the aim of the other. The two parameters together define the ‘form’ of the object studied. The shape is the total of all information invariant under translations, rotations, and isotropic rescaling (Kendall, 1989; Small, 1996). This mathematical framework reveals the geometrical nature of shape; what is conserved as concerns an heart draw on a page, if you rotate the page, change its size uniformly or move the page on your desk, is shape. As regards watersheds, existing methods all make use of the hypothesis that relations between the size-independent shape and the functioning of a watershed are conserved when projected on the plane. This view could probably be costly in terms of information loss, since drainage basin delineation is highly sensitive to digital elevation model (DEM) uncertainty (Oksanen and Sarjakoski, 2005). However, morphometrics on such planar objects is rather common, including in geography (Moellering and Rayner, 1981) and more notably in biology, where insights of great value have been obtained studying the shape of a population of organs/individuals and their changes along individual ontogeny or evolutionary changes (Baylac and Frieß, 2005; Pryer and Hearn, 2009; Terral et al., 2010). There are several methods in use to describe and summarize the parameters, i.e. to obtain a measure of the differences between shapes, and consequently perform univariate or multivariate statistical analyses (Bárdossy and Schmidt, 2002; Gaucherel, 2003; Moellering and Rayner, 1981), but these methods differ in their basic approaches. On one hand, one-dimensional and global metrics, such as concavity, compactness, elongation, symmetry, dextro/levorotorary, etc., have been defined on the basis of the human perception of shape and convenience (Wentz, 2000; Miller and Wentz, 2003). On the other hand, methods that describe and preserve geometric information, e.g. Fourier-based outline analysis, rely on an objective mathematical framework that place corresponding shapes and their descriptors in a bijective relationship (Moellering and Rayner, 1981; Kuhl and Giardina, 1982). For this reason, this method allows shape reconstruction from their descriptors. In other words, while very different shapes can have the same shape metrics (elongation, compactness, etc.), Fourier-based approaches will reveal these differences since the complete geometrical differences between shapes.
5The reasonable hypothesis that a watershed’s boundaries capture part of the information needed to understand its functioning starts to be testable with an accurate method to analyze its two-dimensional shape. Such successful attempt would be the first step towards integrating others important processes such as topography and stream networks. It was our first objective to propose here such a method based on elliptical Fourier analysis that could reveal complementary information to scalar shape metrics. The method as detailed below allows one to describe the object’s outline as closely as needed, as a sum of trigonometric functions. Our second objective was to illustrate possible uses of such a watershed boundary analysis. We analyzed 75 of the biggest watersheds of Haiti, and tried to compare their shape quantification to the commonly used geomorphologic indices (Bárdossy and Schmidt, 2002). The central question here was: what are the real strengths of the Fourier ellipse method? In particular, which correlation may exist between the boundary shapes described this way and the classical geomorphologic measures (Bárdossy and Schmidt, 2002; Gaucherel, 2003). We hypothesized that Fourier ellipses should not only be able to identify obvious shape properties such as watershed elongation, but also uncover a wide range of additional quantitative properties. We finally discussed the method used to characterize the watershed shapes and the properties identified on a unique set of watershed boundaries such as are to be found in the same country.
Fig. 1 – An illustration of the link between the shape of a watershed and its hydrograph.
Fig. 1 – Illustration du lien entre la forme d’un bassin-versant et son hydrogramme.

On the top row are drawn three different watershed outlines with their outlet figured as the dashed arrow. Below, the trends that we are likely to observe if the river discharge was recorded after a rain event. A pear-shaped watershed, as drawn on the left column will have an early discharge peak while it will be delayed for the basin of the middle column. Similarly two peaks will be observed if the watershed is constricted. Redrawn and adapted from K.J. Gregory and D.E. Walling, 1973.
Sur la ligne du haut figurent des bassins versants de différentes formes et la position de leur exutoire est indiquée par la flèche en pointillé. Dessous, les patrons de débit susceptibles d’être observés à l’exutoire après un épisode pluvieux. Un bassin-versant en forme de poire (à gauche) aura un pic de décharge plus tardif que celui du milieu. De la même façon, deux pics seront observés si le bassin-versant est étriqué en son milieu. Redessiné et adapté de K.J. Gregory et D.E. Walling, 1973.
6As part of a project on the characterization of watersheds, our study area is Haiti, a Caribbean mountainous country located 18°-20°N and 71°-74°W that has ~1800 km of coastline and shares an island with the Dominican Republic. Altitudes higher than 200 m occupy roughly 75% of the country’s surface, and more than 80% of the soil has metamorphic and sedimentary origins. The DEM used to extract watershed boundaries here was ASTER GDEM v2, a product jointly developed by METI of Japan and NASA of the US (Tachikawa and Hato, 2011), and released in 2011. The model has a one arc second elevation grid (approximately 30 m at the equator). After filling spurious sinks, we used a single eight-direction (D8) algorithm to extract the flowing direction. The draining direction was assigned according to the steepest downward slope in a 3×3 neighborhood (O’Callaghan and Mark, 1984), and delineation of watershed boundaries followed the ridgelines from outlets. Only watersheds with an area above 50 km² each were used in this analysis, gathering 75 outlines for shape analysis and approximately 85% of Haiti (fig. 2).
Fig. 2 – Watershed outlines and map of Haiti.
Fig. 2 – Contours des bassins versant et carte d’Haïti.

A: Outlines of the 75 watersheds used in this study. The outlines are scaled so that they appear to be of the same size. The point indicates the outlet location. B: Map of Haiti and the studied watersheds. 1: outlets; 2: Haiti-Dominican Republic border; 3: watersheds; 4: inter basins; 5: Dominican Republic.
A : Contours des 75 bassins versants étudiés dans cette étude. La taille des contours est ajustée pour les besoins de l’illustration. Le point indique, pour chaque bassin, la position de l’exutoire. B : Carte d’Haïti avec les bassins versants étudiés. 1 : position des exutoires ; 2 : frontière entre Haïti et la République Dominicaine ; 3 : bassins versants étudiés ; 4 : bassins versants non étudiés ; 5 : République Dominicaine.
7Watershed outlines were analyzed using the elliptical Fourier analysis approach. The steps involved in the process will not be extensively described as published reference books and papers detail them (Giardina and Kuhl, 1977; Kuhl and Giardina, 1982; Claude, 2008). The basic principle was to fit a Fourier series on the x and y outline coordinates of the Cartesian plane as a function of the curvilinear abscissa (i.e., along the watershed outline).
8The two parametric functions x(t) and y(t) thus define T-periodic functions where T is the outline perimeter. One sets ω = 2π/T and then t, the curvilinear abscissa, varies from 0 to T. One can now express x(t) as:
with
an and bn are called harmonic coefficients.
y(t) can be expressed similarly by replacing
an and bn in the above expressions with
cn and dn, respectively. In practice, watershed outlines are closed polygons with a k finite number of points that are exactly fitted by k/2 harmonics. Discrete estimators for the harmonic coefficients of the nth harmonic are calculated as follows:
9with

10Again, c0, cn and dn are computed similarly (Kuhl and Giardina, 1982). Intuitively, for all positive integers n, the sum of a cosine curve and a sine curve represent the nth harmonic content of the x and y projections of the k-edged polygon, and for any n, these two curves define an ellipse in the plane. Ferson and colleagues noticed that in the “time” it takes the nth harmonic to traverse its ellipse n times, the (n+1)th harmonic has traversed its own ellipse n+1 times. The reconstruction of the original polygon is done by vector adding these ellipses for all harmonics, which echoes Ptolemy’s epicycles (fig. 3), and the reconstitution obtained from N harmonics is the best fit possible in a least-squares sense (Ferson, Rohlf, and Koehn, 1985). Four coefficients per harmonic are then obtained. We used the first harmonic, that is also the best fitting ellipse, to normalize the harmonic coefficients so that they can be invariant to size and rotation. The harmonic coefficients can also be normalized, and usually are, for the location of the first outline coordinate. If so, the shapes are individually aligned according to their first ellipse. If not, a homologous point has to be defined for every analyzed outline, thus defining for them all the first outline coordinates. In other words, if there is a rationale for considering that the successive k coordinates sampled along the outline share a common denominator in the processes leading to the shapes observed, the location of the starting point has to be conserved. Both cases, with and without a homologous point, are explored.
11Two separate analyses were performed on the 75 watersheds previously obtained. First, we normalized the Fourier coefficients for the location of the outlet to obtain a global description of the watershed shapes per se with no regard to the outlet location. Then, we conserved this information by not normalizing the Fourier coefficients for the outlet location. Indeed, we can consider that the outlet is a characteristic point of the watershed. Consequently, it should constrain its associated watershed shape.
12The number of harmonics retained in the analysis was estimated using both the harmonic power and, visually, the efficiency of the outline reconstruction. The cumulative sum of the harmonic power (half the sum of the squared harmonic coefficients) indirectly reflects the amplitude of the ellipses, while the outline reconstruction usually serves as a ballpark estimation of the required number of harmonics. For the sake of comparing Fourier elliptical descriptors with the classical shape indices, the most common ones have also been computed on the watershed outlines, namely
Gravelius
form
circularity
lemniscate
and elongation indices
(as reviewed in Bàrdossy and Schmidt, 2002).
13Principal component analyses (PCA) were performed on the matrices of harmonic coefficients. We did not rescale every coefficient and consequently: (i) high-order harmonics ranked lower than low-order harmonics in the global variance explanation and (ii) the number of harmonics played only a marginal role in the results obtained. Percentages of the variance explained by the successive PC axes were calculated using the eigen values of the variance/covariance matrix. Three PCAs were performed on the matrix of Fourier harmonic coefficients, (i) without and (ii) with outlet conserved in the watershed outlines, and (iii) classical shape indices combined with Fourier coefficients with conserved outlets. All statistical analyses were done using R 2.15.0; the package Momocs v. 0.1 dedicated to shape analysis and ade4 for PCA (Dray and Dufour, 2007; Bonhomme et al., 2012; R Development Core Team, 2012).
Fig. 3 – A graphical illustration of the Elliptical Fourier analysis.
Fig. 3 – Illustration des transformées elliptiques de Fourier.

Ellipses of higher orders carry less and less information and “roll” over ellipses of lower orders to describe/reconstruct the outline.
Les harmoniques définissent successivement des ellipses qui « tournent » sur les ellipses des harmoniques précédentes. Elles apportent de moins en moins d’information pour la description et la reconstitution du contour.
14Thirty-six points, equidistantly distributed along the curvilinear abscissa, were sampled on each of the 75 watershed outlines used in the analysis, since 18 harmonics accounted on average for 99.99% of the cumulated harmonic power, they were thus chosen for the shape analysis. On average, the original outlines were defined by 3134 coordinates (SD = 3388; min = 1136; median = 2145; max = 23470).
15As expected, the PCA statistical analysis based on non-conserved outlet watersheds spread the variance among a large number of axes without a clear dominance of any shape property (fig. 4A, inset). The first PC axis (35% of the explained variance) exhibits the already well-known elongation property (fig. 4A). The second PC axis (18%) shows a curvature property of the central axis (the major river) of the watershed, being levorotary or dextrorotary (i.e., turning left or right, respectively). This second axis brings additional information than this curvature property, as the positive and negative values along to this axis are not perfectly symmetrical and may exhibit additional shape subtleties (fig. 4A). As we do not know in this statistical analysis where the outlet is, it was not possible to draw conclusions regarding the possible symmetry of the watershed, while it was in the case of its curvature.
16The PCA performed on conserved outlet watersheds seems to have captured some of their dominant properties according to the distribution of the variance explained by the successive axes (fig. 4B, inset). The first PC axis is interpreted as the watershed symmetry along its major river axis, as the outlets are always located at the right side of the figure. This PC axis indeed depicts the outlet’s orientation (73% of the explained variance). The second PC axis, while it explains an important part of the residual variance (13%), is much more difficult to interpret (fig. 4B and C). We do not have any words to describe such a shape property, although it seems related to the regularity of the outline. The width of the boundaries close to the outlet (right-hand side) seems to vary along this second PC axis, relatively to the width far from the outlet (left-hand side). So, in a certain sense, this shape property captures the lowland spatial distribution within the watershed. The horseshoe effect observed on the first two PC axes probably reflects the fact that the same irregular watershed may have a right or a left symmetry. The third PC axis, relatively obvious, is related to the basin’s elongation (fig. 4C). Yet, it has here lower importance when outlets are conserved, as it now concerns the watershed elongation along to its central axis.
17This detailed shape analysis does not highlight the real potential of the Fourier elliptical approach in terms of shape quantification. Rather, this potential is partially revealed by the PCA done on the matrix gathering, for the 75 watersheds, both the projections of the first three PC axes in the previous PCA plus the five classical shape indices (fig. 4D). In this PCA, the PC3 is confirmed as a component capturing the elongation property (and for example opposed to the Gravelius index). Yet, the symmetry (PC1) and regularity (PC2) are clearly carrying new information on watershed shapes, fully complementary to that already computed with the commonly used shape indices. The third PC axis (not shown) opposes the two latter properties (symmetry and regularity), thus showing that they capture complementary information (not shown).
Fig. 4 – Multivariate analyses of the shape descriptors.
Fig. 4 – Analyses multivariées des descripteurs de forme.

Principal component analysis (PCA) calculated on the matrix of Fourier harmonic coefficients. A: Without conserving outlet location (principal component 1 and 2, further abbreviated PC, are shown). B: With the outlet location conserved (PC1 and PC2). C: With the outlet location conserved (PC2 and PC3 are shown). Insets on A, B, and C correspond to the percentage of the variance explained by the successive PC axes. Points correspond to the position of the 75 watersheds on the PC axes shown. Basin shapes are reconstructed from coordinates sampled on the corresponding PC axes, and illustrate the morphological space. D: PCA calculated on the global shape indices (Gravelius, lemniscate, form, elongation, and circularity) and the three first PC from the previous PCA. Projection of the variables on the two first PC is shown.
Analyses en composantes principales (ACP) calculées sur la matrice des coefficients harmoniques de Fourier. A : Sans conserver la position de l’exutoire (les composantes principales 1 et 2, abrégées ensuite CP, sont montrées). B : En conservant la position de l’exutoire (CP 1 et 2). C : En conservant la position de l’exutoire (CP 2 et 3). Les médaillons des fig. A, B et C correspondent au pourcentage de variance expliqué par les premières CP. Les points correspondent eux à la position de 75 bassins versants sur les CP montrées. Les formes de bassin sont reconstituées à partir d’un échantillon régulier sur les CP correspondantes. Elles illustrent l’espace morphologique. D : ACP calculées sur les indices de forme (Gravelius, lemniscate, forme, élongation et circularité) et sur les trois premières composantes de la précédente ACP. La projection des variables sur les deux premières CP est illustrée.
18In this study, we analyzed the boundary shapes of 75 watersheds approximately covering ca. 80% of the territory of Haiti. Each of them had an area greater than 50 km² and had been extracted from a finely-tuned and homogeneous methodology from the available DEM. This is, to our knowledge, the first time that watershed boundaries have been quantified and analyzed extensively, utilizing the power available in the Fourier elliptical approach. This approach enables one to fully reconstruct each boundary from its descriptors, and captures all the geometric information needed from its shape.
19It appeared from the PCA that three shape properties may characterize the Haitian watersheds: (i) basin asymmetry, (ii) basin regularity, and (iii) basin elongation, in order of decreasing variance explained. The asymmetry relates to the side on which the boundaries are curved beside the main watershed axis. The basin regularity is more difficult to interpret and has never been mentioned, to our knowledge, in the literature: it expresses regularity in terms of concavities and convexities of the outline, as well as a differential width between upstream and downstream. This is why we hypothesize that it may be related to the plain (low-elevation) spatial distributions close to the outlet of the watersheds studied. Yet it remains to be tested, such a shape property may have profound implications for the watershed clock (the water flow timing) and for the discharge measured at the outlet. A watershed that is larger at its outlet than upstream will have a higher reactivity and more rapid floods than in the opposite case. If this view is confirmed, the shape property should be studied in more detail for its hydrological consequences. Elongation is the most studied shape property, and is also retrieved from this analysis.
20Moreover, our method taking into account for the position of outlet is, to our knowledge, the only one able to detect the difference between two watersheds with the same boundary shape (i.e., with the same global indices), but outlets at different positions. Two elongated watersheds, one with outlet on the major axis of the best fitting ellipse and another with the outlet on the minor axis of it, will exhibit different hydrological behaviors. The first one will show a peak delay and spread the river discharge, while the second one will likely show a higher discharge peak. Hence, Elliptical Fourier Analysis is able to quantify the elongation by taking into account the position of the outlet.
21The ultimate goal of morphometrics is to provide insights into the underlying processes, exemplified in this study as a better understanding on how water is collected and transferred towards the outlet. Yet, the approach chosen is often much more than a subject for debate between different schools of thoughts. Unless due care is exercised in such cases, it can lead to erroneous conclusions. For instance, the fractal geometry approach challenges the validity of indices such as the Gravelius index based on the area/perimeter ratio, since only the basin surface is a well-defined measure, the perimeter measurement being dependent on the measurement gauge used (Bendjoudi and Hubert, 2002). Our approach, based on the drainage basin delineation, is sensitive to DEM uncertainty (Oksanen and Sarjakoski, 2005) yet it is probably largely circumvented by such Fourier approaches since the coarse trends of the shape contribute far most than the finer details of the shape. In this exploratory study, the elliptical Fourier approach has demonstrated its ability to capture a wide range of shape properties, such as elongation, curvature, and asymmetry. When compared to the more classical and global indices, Fourier-based indices (PC1 and PC2; fig. 4D) appear to offer a realistic complementary quantification of the watershed shapes. In addition, they have a significant advantage over methods in current use: an ability to reconstruct outlines and to model the watershed boundaries for a wide range of purposes. For instance, they can create completely new watershed boundaries (i.e., they neither exist nor are observed). We can then explore the possible and impossible boundary shapes, and locate them into the previously reconstructed morphological space. In that sense, it is possible to model an outline without the various processes that have generated it. It helps to imagine non-existing shapes and to test hypotheses such as: ‘What if the basin was more elongated?’ or ‘What if the basin was constricted in such-and-such a way?’.
22Elliptical Fourier analysis is one of the most powerful tools that may be used to rigorously analyze watershed boundaries, and more generally, closed outlines. While the method has been seen to be more powerful than the other classical global shape-index techniques, its only weakness is that a matrix of harmonic coefficients on its own is not (at all) straightforward in describing shapes it contains. At the same time, we have to deal with the common trade-off in science that opposes ease of use with descriptive power. Concerning watershed studies, we consider that this first Fourier-based attempt calls for further investigation. An integrative study of the hydrological network and the watershed outline, in a given geographical location, should prove to be of particular value in better understanding the possible links between the basin components, and, in a wider context, in providing insights on hydrological behavior and watershed management.
This research was partly funded by the Agencia Española de Cooperación Internacional para el Desarrollo (AECID) and in close collaboration with the Haitian Comité interministériel de l’Aménagement du Territoire (CIAT) and the Haitian Centre National de l’Information Géo-Spatiale (CNIGS). We warmly thank Allan Bailur for help with its presentation in English and three anonymous reviewers who greatly improved our manuscript.